2.1 Des métiers complémentaires

Regroupant près de quarante collaborateurs, Écureuil Gestion est une société de gestion qui couvre un très large ensemble de métiers complémentaires :

• La gestion financière : ce terme regroupe toute la gestion des portefeuilles des OPCVM Écureuil, sur l'ensemble des marchés, dans le strict respect des orientations fixées par les conseils d'administration des Sicav, et des règles dictées par la COB. Le rôle de la Caisse des dépôts est d'apporter son expertise d'opérateur et de dépositaire.
• L'ingénierie financière et développement : ce département s'occupe de concevoir de nouveaux produits et d'aménager la gamme des OPCVM proposés à la clientèle, selon les évolution des marchés, de la réglementation, des besoins et comportements de la clientèle.
• La gestion de la vie sociale, administrative et comptable des OPCVM : ce bureau est en charge du montage juridique des nouveaux produits, de l'organisation des conseils d'administration des Sicav et des assemblées générales d'actionnaires, des relations avec les autorités de marché et enfin de la tenue de la comptabilité de chaque OPCVM.
• La formation et l'information du réseau de vente : la mise en place d'un dispositif d'information périodique et de programmes de formation, permet à Écureuil Gestion d'entretenir des relations étroites et régulières avec les Caisses d'Épargne.
• La communication clientèle : Son but est d'informer les souscripteurs et de promouvoir les OPCVM. Elle privilégie une information large, régulière et argumentée, complétée par des opérations publicitaires ponctuelles (principalement dans la presse).

2.2 Une équipe jeune et dynamique

2.2.1 Les gérants : un des poumons de la société

A la fois gestionnaires, économistes et stratèges, les gérants d'Écureuil Gestion se situent au coeur même du fonctionnement opérationnel de la société. Aidés dans leur tâche par des assistants de gestion très réactifs et très efficaces, ils gèrent les différentes OPCVM des Caisses d'Épargne en respectant autant que faire se peut la politique et les lignes directrices qui ont été définies. Leurs formations d'origine sont très diverses et on trouvent aussi bien des anciens traders que des Sales en produits structurés ou encore des anciens assistants de gestion. Mais, loin d'être un handicap, cette diversité représente à la fois une richesse et une force. Elle permet de confronter les expériences respectives et ainsi d'améliorer les analyses nécessaires des marchés.

2.2.2 Des assistants très réactifs

L'assistant de gestion est une pièce maîtresse dans le grand échiquier de la gestion. Il doit d'une part, être attentif aux besoins et aux interrogations des gérants en matière de sensibilité et de risque, et d'autre part, réfléchir aux outils qui seraient susceptibles d'améliorer d'une manière ou d'une autre la gestion effective des portefeuilles. Mais, sa mission ne s'arrête pas là car il doit quotidiennement enregistrer, et ce dans des laps de temps très courts, toutes les opérations effectuées par les gérants et les transmettre au Back Office pour que les comptables les enregistrent à leur tour. La journée type d'un assistant de gestion n'est donc pas de tout repos et se caractérise à la fois par de très fortes contraintes temporelles et par une très grande liberté d'action.

2.2.3 De relativement bonnes conditions de stage

Intégré au département  Risk Management, ma mission principale était de réfléchir au développement d'un outil d'aide à la décision et d'un outil de gestion du risque basé sur une méthodologie Value at Risk. Les moyens techniques mis à ma disposition étaient bien adaptés et j'ai pu disposé de tous les outils informatiques nécessaires (RATS pour la modélisation, GAUSS et Excel pour les simulations, Visual Basic et une formation en VBA pour le développement d'outils professionnels) et d'une expertise économique et financière efficace.

Sur le plan humain, il règne au sein de cette société une atmosphère de travail très conviviale et s'il existe un point commun entre les différentes personnes qui compose le département, c'est sans aucun doute la disponibilité. Il arrive bien évidemment que l'atmosphère se tende quelque peu certains jours d'annonce, mais cela ne change en rien les relations existantes.

3.1 Problématique

Il s'agit de proposer un modèle économétrique permettant de rendre compte de la dynamique d'un ensemble de variables macro financières sensibles dans la gestion d'un portefeuille. Ces variables représentent les principaux facteurs de risque, corrélés et évolutifs, auxquels sont confrontés les gérants dans leur travail quotidien. Ce modèle constitue le coeur d'un outil d'aide à la décision, utile pour une analyse rétrospective, pour une évaluation de la conjoncture courante, ou dans un but prospectif, pour définir des stratégies de gestion à l'horizon d'un an, ou plus, sous réserve de l'élaboration de scénarii macroéconomiques.

Dans l'analyse qui est menée, nous considérons que les variables telles que les rendements d'obligations de différentes maturités pour différents pays, les indices boursiers de différentes places ainsi que les taux de change entre les principales devises présentent des évolutions dynamiques qui partagent des tendances dites de long terme par opposition aux fluctuations transitoires qui peuvent être observées. L'identification de telles tendances s'avère extrêmement utile pour décrire les facteurs de risques dont il a été question, d'une part parce qu'elles apparaissent en nombre plus réduit que les variables initiales, d'autre part parce qu'elles permettent de décrire efficacement les risques persistants, dont l'appréhension est déterminante dans l'élaboration d'une stratégie de gestion de moyen ou de long terme.

3.2 Notions de tendance et de choc

A chaque instant, la dynamique d'une variable X évolue sous l'effet d'un choc qui correspond à une "surprise", estimée, de ce fait comme plus petite partie imprévisible c'est-à-dire l'innovation de la variable à la date concernée ...

4.1 Une théorie bien définie

Le risque de marché représente le risque auquel est confronté un investisseur en raison de l'incertitude qui pèse sur les évolutions défavorables du cours des titres qu'il possède dans son portefeuille. De ce fait, un critère d'évaluation du risque de marché tel que la VaR ne doit prendre en compte que le risque de perte.

4.1.1 Une définition simple

Considérons un actif dont la valeur à un instant t est notée V_t. On définit alors la perte² subie sur cet actif durant une période [s;t] par

Ls,t = Vs - Vt

On suppose par ailleurs que la valeur de cet actif et donc des pertes associées à cet actif évoluent de manière stationnaire. Ainsi on peut remplacer l'intervalle [s;t] par l'intervalle [0;t-s] et la variable L n'aura plus pour indice que la seule durée de l'intervalle.

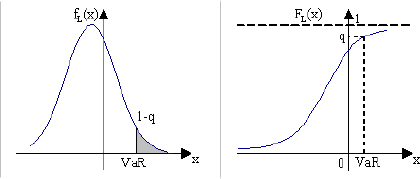
La Value at Risk de l'actif pour la durée t et le niveau de probabilité q se définit comme la perte encourue maximale sur cet actif durant l'intervalle [0;t] pour une probabilité de (1 - q) :

Pr [Lt > VaR] = 1 - q         Û          Pr [ Lt £ VaR] = q

Il existe donc deux paramètres dans la définition de la notion de VaR : la durée t et la probabilité q. En pratique, on fixe une fois pour toute la durée de calcul de la VaR (un jour, une semaine ou un mois) et on calcule la VaR³ en fonction de la probabilité q.

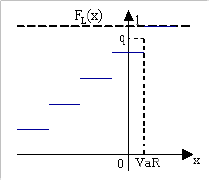
Toutefois, cette définition pose un certain nombre de problèmes liés notamment à l'existence et à la caractérisation de la fonction de densité. Pour les variables discrètes par exemple, la VaR n'est pas définit de façon précise et dans le cas où q correspond à un saut de la fonction de répartition, aucune valeur de la perte ne peut convenir.

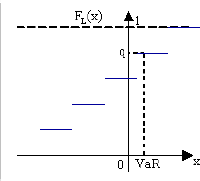
De la même manière, lorsque q correspond à un palier de la fonction de répartition, une infinité de valeurs conviennent et on choisit, par sécurité, de prendre la valeur la plus défavorable, c'est à dire la plus grande.

De ce fait, la définition rigoureuse de la VaR s'écrit alors sous la forme :

VaRq = max ì í î V : Pr [Lt £ V] £ q ü ý þ

Remarque : lorsque la variable aléatoire L_t suit une loi normale de moyenne m et d'écart type s, on peut écrire :

Pr é ë Lt - m s £ VaRq - m s ù û = q

Et si on note z_q le quantile d'ordre q de la distribution normale, on obtient une formule très simple de la VaR :

VaRq = m + zq s

4.1.2 VaR d'un portefeuille

Considérons un portefeuille constitué de N actifs en nombre respectifs n₁,... ,n₂. Si on note p_j le prix du j^ème titre et p_p le prix du portefeuille, la variation relative de prix du portefeuille obéira à la relation :

Dpp = N å j = 1  njDpj

où Dp = (p_t - p_{t - 1}) / (p_{t - 1}).

Le choix d'une variation relative sur une variation absolue permet d'une part de relativiser le poids des différents facteurs pouvant intervenir dans l'évaluation d'un portefeuille, et d'autre part, de fournir une variable pouvant posséder certaines propriétés distributionnelles.

Mais, il n'est en général pas possible de déduire la loi de probabilité du portefeuille et ce même si on connaît la distribution des différents Dp. La loi de probabilité d'une somme de variables aléatoires n'est aisée à déterminer que si celles-ci sont indépendantes, ce qui n'est bien évidemment pas le cas ici.

Cependant, si on suppose une distribution normale du portefeuille, on peut aisément déterminer la VaR de ce dernier à partir des deux premiers moments :

VaRq = - E[Dpp] + zq s(Dpp)

On détermine alors les deux premiers moments de la distribution des variations du portefeuille :

E[Dpp] = N å j = 1  nj E[Dpj] Var(Dpp) = N å i = 1  N å j = 1  ni nj Cov(Dpi, Dpj)

Remarques : L'utilisation de cette relation présente cependant deux inconvénients majeurs : d'une part, elle suppose la normalité de la distribution du portefeuille, et d'autre part, elle nécessite de connaître un grand nombre de paramètre (au total N*(N+3)/2).

En pratique, la loi de distribution des portefeuilles est rarement normale et possède des queues de distribution beaucoup plus épaisses que celles d'une loi normale⁴. Les distributions leptocurtiques, les lois de Laplace et les lois astables de Levy sont généralement plus appropriées.

Par ailleurs, la taille des portefeuilles dans les sociétés de gestion est en général très importante (une centaine de lignes environ) et ce pour des soucis de réduction du risque globale par diversification. Dans le cas d'un portefeuille possédant N = 100 titres différents par exemple, il faut connaître un nombre de paramètres très important : au total 100*(100+3)/2 = 5150.

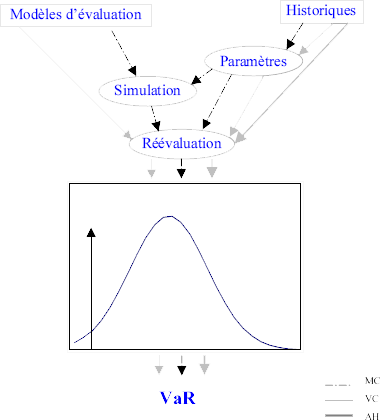
4.2 Estimation de la VaR

La présentation du critère VaR telle que nous l'avons faite, montre qu'il est relativement aisé de déterminer la VaR dès lors que l'on connaît la fonction de répartition de la variable aléatoire "perte". Trois méthodes de calcul de la VaR ont fait leur preuve à l'heure actuelle : la méthode de l'analyse historique, la méthode de la matrice des variances-covariances estimée et la technique de simulation de Monté Carlo. Les trois hypothèses principales qui permettent de différencier ces techniques d'estimation portent sur la distribution des prix des actifs, sur les modèles d'évaluation des prix des actifs et enfin sur la stationnarité des variations de prix des différents facteurs de risque.

Les schémas directeurs de ces trois méthodes d'estimations sont résumés dans la figure ci-dessous :

4.2.1 Une première étape obligatoire

L'étape préliminaire consistant à choisir les facteurs de risque sur lesquels vont être projetés les différentes lignes des portefeuilles est primordiale. Il existe, en effet, un nombre important de titres et de produits dérivés, et ce, sur différentes places boursières. Donc un nombre important de taux de change et un nombre tout aussi important de maturités possibles pour ces produits. De plus, toutes ces caractéristiques peuvent être combinées et donner ainsi une infinité de titres possibles.

Le choix des facteurs de risque est l'un des problèmes les plus épineux que nous ayons rencontré. Il faut, en effet, effectuer un savant arbitrage entre la précision des résultats, la cohérence des facteurs retenus, leur interprétabilité par les gérants et une économie des moyens de calculs.

De ce fait, les facteurs de risque que nous avons décidé de retenir ne concerne que cinq pays : l'Allemagne, les États-Unis, la France, le Japon et le Royaume Uni. On trouve :

• Un taux directeur de la courbe des taux : le taux à deux ans pour les Etats-Unis, le Japon et le Royaume Uni, et le taux à trois mois pour l'Allemagne.
• La courbe des taux via certains spreads (sauf pour la France).
• Les taux de change par rapport au Dollar (sauf pour la France).
• Un indice boursier (DAX, S&P500, CAC, NIKKEI et FSTE).

Remarque : Pour la méthode de la matrice de variances-covariances estimée, RiskMetrics^TM propose d'utiliser comme facteurs de risque :

• 30 taux de change et 30 indices boursiers nationaux pour la représentation des actions à l'aide de leur  bêta.
• 14 points de la courbe des taux d'intérêt zéro-coupon pour la représentation des instruments à taux fixe comme les obligations.
• un panel représentatif de matières premières.

4.2.2 Des besoins spécifiques

Écureuil Gestion a des besoins très spécifiques en matière de gestion du risque et nous avons été contraint de choisir la méthode qui satisfasse au mieux les attentes des gestionnaires. De ce fait, nous ne ferons ici qu'une présentation des méthodes de la matrice des variances-covariances estimée et de l'analyse historique, et justifierons notre choix pour la méthode de Monté Carlo.

4.2.3 Méthode de la matrice des variances-covariances estimée

La méthode de la matrice des variances-covariances estimée est à ce jour la plus utilisée dans le monde et ce grâce à une banque américaine : JP. Morgan. Le développement de cette méthode par JP. Morgan dans le début des années 1980 a permis à la Value at Risk de connaître son succès actuel. D'ailleurs, il arrive très souvent que les spécialistes appellent cette méthode la "VaR JP. Morgan".

Cette technique nécessite préalablement à son calcul deux étapes importantes : tout d'abord, la détermination des facteurs de risque en lesquels les actifs présents dans les différents portefeuilles peuvent être décomposés, et ensuite la répartition des différents cash-flows associés à ces facteurs de risque.

Des hypothèses contraignantes :

Tous les fondements de cette méthode reposent sur la normalité des facteurs de risque et des rendements des différents actifs. Cette hypothèse permet, en effet, de simplifier énormément le calcul de la VaR puisque cette dernière devient un simple multiple de l'écart type du portefeuille, qui est lui même une fonction linéaire des écarts types et des covariances des différents actifs présents dans le portefeuille.

La méthode présuppose donc l'évaluation des moyennes et des variances de tous ces facteurs. Toutefois, ces moyennes et variances ne sont pas calculer grâce à la méthode historique standard mais suivant une pondération qui accorde plus d'importance aux observations récentes. On définit un l ⁵ compris entre 0 et 1 (plus il est proche de 1 et plus le passé proche est important) et on calcule les paramètres suivants :

s12 = (1-l) T å j=1  lj-1 æ è Rt-j- R   ö ø 2   s12,t = (1-l) T å j=1  lj-1 æ è R1,t-j- R   1  ö ø æ è R2,t-j- R   2 ö ø

Cette pondération permet de ne pas garder en mémoire toutes les données intervenant dans les formules. En effet, si on suppose T très grand, on peut facilement obtenir les formules de récurrence suivantes :

st+12 = lst2 + (1-l) æ è Rt- R   ö ø 2   s12,t+1 = ls12,t + (1-l) æ è R1,t- R   1  ö ø æ è R2,t- R   2  ö ø

Par ailleurs, si on veut utiliser dans le calcul de la VaR les paramètres obtenus lors de l'estimation sur un échantillon des variations de prix passées, il est nécessaire de supposer la stationnarité des processus considérés.

Calcul de la VaR pour un portefeuille de valeurs linéaires

Considérons un portefeuille constitué de N actifs⁶ en nombres respectifs n₁,...,n_N s'exprimant à partir des facteurs de risque X₁,...,X_n :

pj = aj1 X1 + ... + ajn Xn        j = 1,...,N

La valeur du portefeuille s'écrit

pp(t) = N å j = 1  nj pj(t) = n å k = 1  æ è N å j = 1  nj ajk ö ø Xk(t)

et ses variations entre les dates t - 1 et t

Dpp(t) = n å k = 1  æ è N å j = 1  nj ajk ö ø ( Xk(t)-Xk(t-1) ) = n å k = 1  æ è N å j = 1  nj ajk Xk(t-1) ö ø Xk(t) -Xk(t-1) Xk(t-1) = n å k = 1  xk(t-1) Dk(t)

où x_k(t-1) peut s'interpréter comme le montant investi en (t-1) dans le k^ième facteur de risque.

On suppose que l'horizon de calcul de la VaR est l'époque 1 et que la période à laquelle on effectue les calculs est l'époque 0. On suppose également connus :

Les positions actuelles en les différents facteurs de risque :

xk(0) = xk        k = 1,...,n

L'estimation des moyennes et variances historiques :

E[ Dk(1) ] = Ek                     k = 1,...,n Var( Dk(1) ) = sk2 = skk            k = 1,...,n Cov( Dk(1) , Dl(1) ) = skl                     k,l = 1,...,n

Et on calcule ainsi la VaR grâce à l'équation:

VaRq = -E[ Dpp ] + zq s( Dpp ) = - n å k = 1  xk Ek + zq   æ Ö n å k = 1  n å l = 1  xk xl skl

Cas particulier des actions

On traite les actions par un modèle comparable au modèle à indice simple de Sharpe. Ce modèle postule que la variation de prix d'une action est une fonction du premier degré de la variation d'un indice représentatif du marché.

Dpj = aj + bj DI + Dej        j = 1,...,N

où a et b ⁷ s'évaluent par les techniques standards de régression.

Dans ce cas, il est facile d'obtenir :

VaRq = -a P - bP EI + zq   æ Ö bP2 sI2 + N å j = 1  nj2 sej2

Calcul de la VaR pour un portefeuille de valeurs non linéaires

Les produits non linéaires représentent un réel problème pour la technique de la matrice des variances-covariances estimée car l'application de cette méthode est basée sur le fait qu'une combinaison linéaire de variables normales est distribuée suivant une loi normale.

Pour palier à ce problème, on suppose que les variations de prix du sous-jacent sont distribuées suivant une loi normale et on effectue un développement de Taylor du modèle d'évaluation retenu. Il convient de pousser le développement jusqu'à l'ordre 2 afin de tenir compte des évolutions de prix du sous-jacent.

On va considérer plus particulièrement le cas d'une option évaluée grâce à la formule de Black & Sholes :

Dpt = fS'¢(St,K,t,st,RF) DSt + 1 2 fSS"¢¢(St,K,t,st,RF) (DSt)2+fK'¢(St,K,t,st,RF) DK + ft'¢(St,K,t,st,RF) Dt + fs'¢(St,K,t,st,RF) Dst + fR'¢(St,K,t,st,RF) DRt = D.DSt + 1 2 G.(DSt) 2 + fK'¢.DK - Q.Dt + V.Dst + P.DRt

Dans la pratique, on se limite principalement aux paramètres D, G et Q :

Dpt = D.DSt + 1 2 G.(DSt)2 - Q.Dt

La distribution de Dp_t est ensuite déterminée en recherchant dans la famille des distributions de Johnson, celle qui égalise les quatre premiers moments de Dp_t :

E[ Dpt ] = 1 2 G.st2 - Q.D t Var( Dpt ) = D2.st2 + 1 2 G2.st4 g1( Dpt ) = G.st (3D3 + G2.st2) æ è D2 +  1 2 G2.st2 ö ø [3/2]   g1( Dpt ) = 3 é ë (1-D4) + 3D2.G2.st2 +  3 4 G4.st4 ù û D2 +  1 2 G2.st4

Plus précisément, parmi les quatre relations

DSt = a + b Dpt-c d DSt = a + b.ln æ è Dpt-c d ö ø DSt = a + b.arcsinh æ è Dpt-c d ö ø DSt = a + b.ln æ è Dpt-c c + d-Dpt ö ø

qui définissent respectivement des lois normales, lognormales, non bornées et bornées. On détermine la loi et les paramètres a, b, c, d tels que DS_t suit une loi normale de moyenne nulle et d'écart type s_t.

On reprend ensuite la définition initiale de la VaR basée sur le quantile

Pr [ Lt £ VaR ] = q

et on résout l'équation S_t = - z_q par rapport à Dp_t.

En conclusion  

La présente méthode d'évaluation de la VaR détermine, dans un premier temps, le paramètre VaR pour chacun des facteurs de risque séparément, puis dans un deuxième temps, les agrège par l'intermédiaire de la matrice des variances-covariances estimée. De ce fait, cette méthode est souvent présentée comme une "méthode locale" de calcul de la VaR en opposition avec les méthodes qui déterminent directement la VaR du portefeuille sans calculer celles des facteurs de risque pris séparément.

La méthode de la matrice des variances-covariances estimée est donc une bonne méthode à condition que les hypothèses de base (normalité conditionnelle, linéarité, stationnarité) soient satisfaites. Pour cela, il est parfois nécessaire d'effectuer un traitement particulier sur certains titres complexes (les options par exemple). Mais, le principal reproche de cette méthode est qu'elle demande un volume très important de données.

4.2.3 Méthode historique

La méthode d'estimation de la VaR par analyse historique repose sur l'hypothèse que la distribution des variations de prix observée à partir de l'historique va se reproduire dans l'avenir. Dans les faits, cela revient à supposer que les variations de prix des différents facteurs de risque sont stationnaires.

Comme précédemment, il convient de bien identifier les facteurs de risque qui nous permettrons de déterminer la valeur des actifs en portefeuille.

On évalue ensuite les variations relatives de chaque facteurs de risque :

Dk(t) = Xk(t) - Xk(t-1) Xk(t-1)         k = 1,...,n         t = -T+1,...,0

Les données présentes nous permettent alors d'estimer la distribution des valeurs futures des facteurs de risque

Xk(t) (1) = Xk(0).(1+Dk(t))        k = 1,...,n         t = -T+1,...,0

et donc la distribution de la perte encourue

Lk(t) = Xk(0) - Xk(t)(1) = - Dk(t).Xk(0)         k = 1,...,n         t = -T+1,...,0

Cas particulier d'un actif

Considérons un actif dépendant de plusieurs facteurs de risque p = f(X₁,...,X_n) dont on souhaite déterminer la VaR. On évalue les variations futures des facteurs de risque X₁^(t)(1),...,X_n^(t)(1) en utilisant la méthode ci-dessus. De là, on déduit une estimation de la distribution du prix futur de l'actif

p(t)(1) = f( X1(t)(1),...,Xn(t)(1) )         t = -T+1,...,0

et par différence, une estimation de la distribution de la perte subie

L(t) = p(0) - p(t)(1)          t = -T+1,...,0

Quelques remarques importantes

Dans le cas d'un portefeuille, la méthode est similaire à celle d'un actif isolé. On termine simplement l'estimation de la VaR en déterminant la distribution de la perte subie par le portefeuille

L(t) = pP(0) - pP(t)(1) = N å j = 1  nj pj(0) - N å j = 1  nj pj(t) (1)

Il est déconseillé de calculer la VaR en utilisant la formule suivante

VaRq = E[ Lt ] + zq.s(Lt)

car cette dernière suppose la normalité de la distribution alors que cette méthode en est indépendante.

La CHASE MANHATTAN BANK N.A., dans son système Risk^TM d'évaluation de la VaR, propose pour le calcul d'une VaR à 1 jour d'utiliser un historique de T = 100 jours.

Exemple d'un portefeuille action

Considérons un portefeuille constitué de cinq actions en nombres respectifs

n1 = 3,  n2 = 2,  n3 = 5,  n4 = 4,   n5 = 6

pour lesquels on a observé les cours à 11 époques (T=10).

t	C1	C2	C3	C4	C5
-10	12800	23475	1238	2800	129
-9	13150	23150	1236	2765	134
-8	12150	21875	1168	2715	145
-7	11100	21400	1234	2689	168
-6	11725	22100	1310	2599	179
-5	11950	21650	1262	2465	168
-4	12025	22650	1242	2536	164
-3	12325	21000	1170	2497	171
-2	13675	23625	1260	2468	176
-1	14300	24150	1342	2500	165
0	14800	25825	1530	2365	160

On calcule les variations relatives D_k(t) pour t = -9,...,0 :

D1(-9) = 13150 - 12800 12800 = 0.0273

t	Delta1	Delta2	Delta3	Delta4	Delta5
-9	0,027	-0,014	-0,002	-0,013	0,039
-8	-0,076	-0,055	-0,055	-0,018	0,082
-7	-0,086	-0,022	0,057	-0,010	0,159
-6	0,056	0,033	0,062	-0,033	0,065
-5	0,019	-0,020	-0,037	-0,052	-0,061
-4	0,006	0,046	-0,016	0,029	-0,024
-3	0,025	-0,073	-0,058	-0,015	0,043
-2	0,110	0,125	0,077	-0,012	0,029
-1	0,046	0,022	0,065	0,013	-0,063
0	0,035	0,069	0,140	-0,054	-0,030

ainsi que les valeurs estimées pour la prochaine période :

X1(-9) = 14800 × ( 1 + 0.0273 ) = 15204.7

t	X1(1)	X2(1)	X3(1)	X4(1)	X5(1)
-9	15204,69	25467,47	1527,53	2335,44	166,20
-8	13674,52	24402,67	1445,83	2322,23	173,13
-7	13520,99	25264,23	1616,46	2342,35	185,38
-6	15633,33	26669,74	1624,23	2285,84	170,48
-5	15084,01	25299,15	1473,94	2243,06	150,17
-4	14892,89	27017,84	1505,75	2433,12	156,19
-3	15169,23	23943,71	1441,30	2328,63	166,83
-2	16421,10	29053,13	1647,69	2337,53	164,68
-1	15476,42	26398,89	1629,57	2395,66	150,00
0	15317,48	27616,17	1744,34	2237,29	155,15

On détermine alors la valeur du portefeuille en t=0 et les estimations des valeurs futures :

pP(-9)(1) = 3×15204.7 + 2×25467.5 + 5×1527.5 + 4×2335.4 + 6×166.2 = 114525.6

t	pP(0)	pP(1)	L
-9	114120,00	114525,59	-405,59
-8	114120,00	107385,78	6734,22
-7	114120,00	109655,38	4464,62
-6	114120,00	118526,87	-4406,87
-5	114120,00	113093,29	1026,71
-4	114120,00	116912,73	-2792,73
-3	114120,00	110917,13	3202,87
-2	114120,00	125946,20	-11826,20
-1	114120,00	117857,54	-3737,54
0	114120,00	119786,55	-5666,55

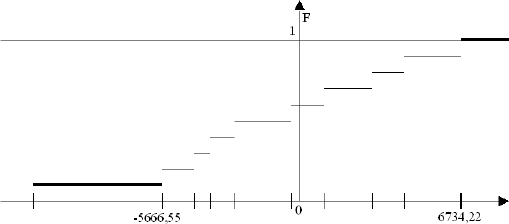
Enfin, la fonction de répartition des pertes permet d'obtenir l'estimation de la VaR.

On déduit ainsi aisément les valeurs :

VaR0.95 = 6734.22 VaR0.05 = -5666.55

En conclusion

Le principal reproche que l'on peut formuler à l'encontre de cette méthode est le suivant : il suffit qu'un petit nombre d'observations sortent de l'ordinaire pour que la valeur de la VaR soit influencer pendant une longue période (égale à la durée des historiques). Ainsi, une erreur de mesure ou une valeur exceptionnelle peuvent avoir des effets désastreux sur l'estimation de la VaR ⁸.

En revanche, cette méthode possède l'avantage d'être une méthode simple, flexible et robuste. Les hypothèses sont peu exigeantes et les données nécessaires peu nombreuses.

4.2.4 La VaR Monté Carlo classique

La simulation de Monté Carlo⁹ est généralement utilisée lorsqu'il est difficile de déterminer la loi de probabilité d'une distribution grâce à un raisonnement mathématique. C'est une technique très puissante mais très lourde à mettre en uvre et il convient d'analyser, comme nous l'avons fait ci-dessus, les différentes approches possibles avant de faire son choix.

Nous présentons ici la méthodologie classique d'estimation de la VaR par la technique de Monté Carlo en l'appliquant tour à tour au cas d'un facteur de risque et d'un portefeuille.

Pour un facteur de risque

Avant de s'attaquer au problème d'estimation de la VaR, il convient de réfléchir plus particulièrement au modèle d'évaluation du facteur de risque que l'on va considérer. Généralement, on retient plusieurs modèles d'évaluation et on choisit pour chaque facteur de risque le modèle qui sera le plus adapté. On retiendra par exemple une distribution normale ou un mouvement brownien géométrique selon que l'on considère le return d'une action ou celui d'une option.

A partir des observations passées du facteur de risque X(t) pour t = -T+1,...,0, on estime les paramètres du modèle d'évaluation relatifs à ce facteur. On peut ensuite simuler un grand nombre M de valeurs futures du facteur de risque

X(t)(1)         t = 1,...,M

et on détermine la loi de distribution de la perte encourue

L(t) = X(0) - X(t)(1)         t = 1,...,M

et ainsi la valeur de la VaR.

Pour un portefeuille

On suppose comme précédemment que les N actifs constituant le portefeuille sont fonctions d'un ou plusieurs facteurs de risque X₁,...,X_n

pj(0) = fj ( X1(0),...,Xn(0) )

Avant de générer les valeurs futures des facteurs de risque, on détermine la matrice de variance-covariance¹⁰ et on effectue une décomposition de Choleski¹¹. On peut ainsi prendre en compte la structure de corrélation des facteurs de risque.

Une fois les X_k^(t)(1) générés, on estime par substitution la valeur future des actifs constituant le portefeuille

pj(t)(1) = fj ( X1(t)(1 ,...,Xn(t) (1) )

et ainsi, la valeur future du portefeuille

pP(1) = N å j=1  nj pj(1) = N å j = 1  nj fj ( X1(t)(1),...,Xn(t)(1) )

Enfin, par différence avec la valeur initiale du portefeuille, on obtient la valeur future de la perte subie

L(t) = pP(0) - pP(t)(1)

En conclusion

L'approche Monté Carlo a deux caractéristiques majeures que ne possèdent pas les approches historique ou de J.P. Morgan et qui ont motivé notre choix :

1. En premier lieu, elle ne suppose aucune hypothèse distributionnelle et notamment aucune hypothèse de normalité. On évite ainsi de sous-évaluer la valeur de la VaR lorsque les distributions ont des queux plus épaisses. Elle ne formule pas non plus d'hypothèse sur la linéarité des prix des actifs.
2. Cette méthode est par ailleurs la seule qui puisse être adaptée au calcul d'une VaR à plus long terme comme le nécessite les SICAV d'Ecureuil Gestion.

4.2.4 La VaR Monté Carlo "Écureuil Gestion"

L'approche Monté Carlo classique de la VaR, telle qu'elle peut être présentée par la Bankers Trust dans son système RaRoc2020^TM, comporte une différence notable avec celle que nous avons décidée de retenir à Ecureuil Gestion. On ne pose en effet aucune hypothèse sur les processus suivis par les facteurs de risque (normalité ou leptocurticité du cours des actions, mouvement brownien géométrique des variations relatives, etc.). Ces derniers ont été modélisés dans la première partie de ce rapport et les seules hypothèses que l'on formule portent sur la distribution des variables fondamentales retenues : la loi de distribution de leurs variations absolues est décrite par une loi normale.

En pratique, notre méthodologie est la suivante :

1. On génère tout d'abord autant d'aléas (de même longueur que la VaR) qu'il n'y a de fondamentaux dans les différents modèles. On utilise un historique pour estimer la matrice de variance-covariance de ces fondamentaux et on peut ainsi prendre en compte les corrélations qui peuvent exister entre ces derniers (décomposition de Choleski).
2. On détermine ensuite les valeurs futures des différents facteurs de risque en se basant sur les modèles économétriques que l'on a déterminés précédemment. On simule pour cela autant de bruit blanc ¹² que d'équation de court terme et on obtient ainsi les variations simulées de chaque facteur de risque.
3. Ces facteurs de risque simulés, on projète ou réévalue, selon le choix de modèle que l'on a retenu, les différentes lignes du portefeuille. Le choix du modèle d'évaluation est réalisé en fonction de la qualité des méthodes de projection et de l'existence ou non d'une formule fermée d'évaluation.
4. Grâce à ces modèles, on calcule la valeur du portefeuille en fin de scénarios et on déduit la perte subie sur la période considérée. On reprend ensuite la première étape et on recommence la procédure autant de fois que nécessaire pour obtenir la précision souhaitée.
5. Enfin, on peut déterminer la distribution des pertes subies et ainsi déduire la valeur de la VaR au niveau de risque voulu et sur la période considérée.

---

Footnotes:

¹ Il n'est pas certain qu'avec la réforme actuelle des Caisses d'Épargne, cette situation reste telle que je l'ai connue.
² Il ne s'agit d'une vrai perte que lorsque la valeur de L_s,t est positive. Dans le cas contraire, il s'agit d'un bénéfice.
³ On notera VaR_q une VaR avec une probabilité q lorsqu'il y aura un risque de confusion.
⁴ Les rendements quotidiens des actions ont par exemple une distribution de Pareto ou de Student.
⁵RiskMetrics^TM utilise en pratique des valeurs de l égales à 0.94 et 0.97 pour une périodicité des observations égale respectivement à 1 jour et à 1 mois. Ces valeurs ont été obtenus en optimisant un critère de qualité des prévisions.
⁶On peut considérer identiquement des obligations, des actions, des positions de change, des matières premières, des swaps d'intérêt et de change, des FRA, ...
⁷Le coefficient b mesure la sensibilité de l'actif en question par rapport à l'indice : plus b est grand, plus une variation sur le marché sera répercutée sur le prix de l'action.
⁸L'approche par la théorie des valeurs extrêmes peut aider à résoudre ce problème.
⁹Pour les méthodes de simulations de Monté Carlo, la précision des paramètres estimés est proportionnelle à [1/(Ön)], n étant le nombre de simulations effectuées. Pour 10.000 simulations, on obtient donc une précision de l'ordre de 1%. Toutefois, il est possible d'améliorer cette précision en utilisant des techniques de réduction de la variance, les principales utilisées étant "l'approche antithétique" et "la méthode d'égalité des moments". Toutes ces techniques sont détaillées dans Boyle, Broadie et Glasserman [1997, pp. 1267-1321] : "Monte Carlo methods for security pricing", Journal of Economic Dynamics and Control.
¹⁰On peut pour cela utiliser l'historique qui a servi à l'estimation des paramètres de leur modèle respectif.
¹¹Soit A une matrice symétrique définie positive, il existe une matrice triangulaire inférieure L à éléments diagonaux strictement positifs telle que

A=LLT

¹²C'est à dire un aléa généré sur la base d'une loi normale centrée et de même variance que celle obtenue lors de l'estimation.